반응형
데이터 분석 과정과 EDA
✤1 데이터 분석의 과정
- 데이터 분석 기획
- 비즈니스 이해 및 목표 설정 : 어떤 것을 이루고자 하는지
- 프로젝트 정의 : 어떤 데이터를 바탕으로 무엇을 예측/측정할 것인지
- 데이터 수집 및 정제
- 분석에 필요한 데이터 수집 방법
- 데이터 전처리 : 수집된 데이터의 정합성, 무결성 등 검증
- 데이터 분석 모델링
- 탐색적 데이터 분석(EDA) : 통계량 및 시각화를 통한 데이터의 특성 파악
- 모델링 : 예측을 위한 수학적, 통계적 모델링
- 평가 및 결론 도출
- 모델링을 통해 생성된 결과를 활용한 결론 도출
- 성능 평가 : 도메인, 비즈니스 요구에 맞는 성능 기준에 따라 위의 과정을 수정하며 성능 개선
- 분석 결과의 활용
- 시스템 구현, 서비스에 활용
- 비즈니스 인사이트
✤2 탐색적 데이터 분석(Exploratory Data Analysis, EDA)
- 의미 : 데이터를 분석하기 전에 수치 요약과 시각화를 사용하여 데이터의 분포, 특성, 관계 등을 탐색하고 이해하는 과정
- 목적 : 데이터의 특성과 패턴을 이해하고, 이상치나 결측치를 파악하며, 변수 간의 관계를 분석하여 향후 분석 및 모델링을 위한 인사이트를 도출하는 것
- 내용
- 기초 통계 분석: 평균, 중앙값, 최빈값, 표준편차 등 기본적인 통계량 확인
- 결측치와 이상치 탐색: 결측값의 분포와 이상치를 식별
- 데이터 분포 시각화: 히스토그램, 박스플롯 등의 차트를 통한 분포 확인
- 변수 간 관계 분석: 산점도, 상관계수 등으로 변수 간의 관계 탐색
✤3 엑셀 실습
- Titanic Dataset - 피벗차트/피벗테이블, 상자수염차트

- Iris Dataset

기초 통계 개념
✤1 고등학교 통계 내용
- 정규분포
- 정규분포 : 평균 µ 와 표준편차 σ 에 대해 평균을 중심으로 좌우대칭의 종모양을 가지는 확률분포중심
- 중심극한정리 : 독립적인 확률변수들의 평균은 항상 정규분포에 가까워진다는 것을 증명
- 표준정규분포 : 평균이 0, 표준편차가 1인 정규분포
- 표준화 : 정규분포를 표준정규분포로 변환하는 방법
- 추론통계 : 통계량을 바탕으로 모수를 추정하는 것
- 모집단 : 조사 대상이 되는 전체 집합
- 모수 : 모집단에 대한 요약된 수치, 값에 대한 평균이나 비율 등
- 표본 : 모집단을 대표하는 모집단의 일부
- 통계량 : 표본에 대한 수치적 요약
- 모평균 µ / 모분산 σ2 : 모집단의 평균/분산
- 표본평균 ¯X / 표본분산 s2 : 표본에 대한 평균/분산
- 모분산은 n, 표본분산은 n-1의 자료수로 나누는 차이 있음
- 표본 추출
- 신뢰도 : 어떤 값이 모평균이라고 믿을 수 있는 정도 (주로 95%, 99%)
- 신뢰구간 : 모평균의 추정 구간
✤2 기술통계
- 기술 통계와 추론 통계
- 기술 통계 (Descriptive Statistics) : 데이터의 간결한 요약 정보, 수치적인 통계량 또는 시각화, 데이터의 특징 파악
- 추론 통계 (Inferential Statistics) : 표본을 이용한 모집단에 대한 추론이 목적, 모집단에 대한 가설을 검정
- 기초통계량
- 중심경향성 : 데이터 분포의 중심을 보여주는 값
- 최빈값 (Mode) : 범주형 자료의 대표값으로 적합
- 중앙값 (Median) : 순서형 자료의 대표값으로 적합, 이상치 영향 적음
- 산술평균 (Arithmetic Mean) : 주로 연속형 자료에 사용, 이상치 영향 클 수 있음
- 가중평균 (Weighted Mean) : 자료의 중요도에 따라 가중치 부여한 평균
- 기하평균 (Geometric Mean) : 성장률 등 이전 시점에 대한 비율에 대한 평균을 구할 때 유용 (e.g., CAGR, 주가상승률)
- 퍼짐정도 : 자료가 얼마나 흩어져 있는지
- 분산 (Variance) : 편차 제곱의 평균
- 표준편차 (Standard Deviation) : 분산의 제곱근
- 범위 (Range) : 최댓값 - 최솟값, 계산이 쉽지만 분포에 대한 정보 없음
- IQR (InterQuartile Range) : 제3사분위수 - 제1사분위수, 한쪽으로 치우친 분포의 퍼짐 정도 확인할 때 주로 사용
- 첨도 : 분포의 뾰족한 정도
- 왜도 : 분포의 좌우 비대칭성 정도
- 중심경향성 : 데이터 분포의 중심을 보여주는 값
✤3 상관관계
- 회귀분석 : 독립변수와 종속변수의 관계를 추정하기 위한 분석 방법, 독립변수의 영향력 판단 가능, 인과관계를 설명할 수는 없음
- 공분산 : 두 변수의 관계를 나타내는 개념, 두 변수의 변동이 어떻게 함께 변화하는지를 측정하는데 사용
- Cov(X,Y) > 0 : 양의 상관관계, Cov(X,Y) < 0 : 음의 상관관계
- Cov(X,Y) = 0 : 상관관계 없음. 공분산이 0이라고 해서 독립은 아님
- 상관계수 : 공분산을 각 변량의 표준편차의 곱으로 나눈 것으로, 공분산을 표준화한 것 ( -1과 1사이의 값 )
기술 통계
✤1 데이터 분포 파악 - Titanic
- Fare 기술 통계량

- 피벗차트 5단위

✤2 이상치 탐지
- IQR 활용
- Q1 - 1.5 * IQR (a) 보다 작거나 Q3 + 1.5 * IQR (b) 보다 큰 값
- 정규 분포가 아닌 (한쪽으로 치우친) 자료
- IF(OR(데이터<(a),데이터>(b)),1,0) 처럼 이용
- 정규분포 활용
- z=(x-m)/s= +-3 일 때의 x값 찾고, 그 범위 벗어난 데이터를 이상치로 판단
- z값이 +-3 범위 밖에 있는 데이터를 이상치로 판단
- Box-plot 이용
추론 통계
✤1 평균/분산/표준편차
- 모분산/모표준편차 : VAR.P() , STDEV.P() 이용
- 표본분산/표본표준편차 : VAR.S() , STDEV.S() 이용
✤2 정규분포 관련 함수
- NORM.DIST(x, mean, standard_dev, cumulative) : 주어진 값이 정규 분포를 따를 때, 해당 값의 누적 분포 함수 또는 확률 밀도 함수 값을 계산
- NORM.S.DIST(x, cumulative) = NORM.DIST(x, 0, 1, cumulative)
- t분포
- 표본의 개수가 30개보다 작을 때 사용
- 자유도가 커짐에 따라(30 이상) t분포는 정규분포에 가까워짐
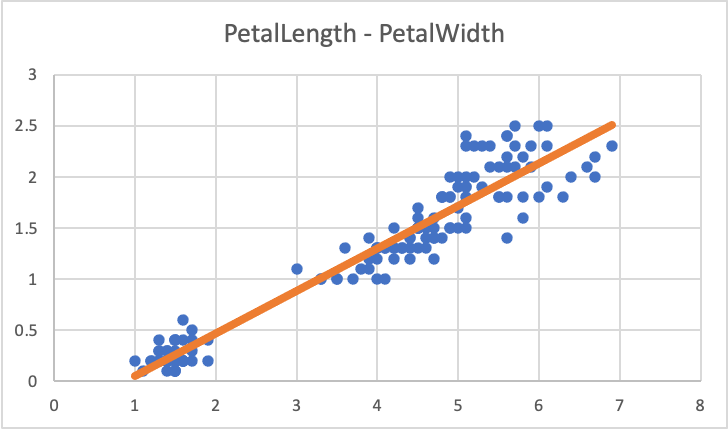
✤3 상관관계 분석 - Iris
- 산점도, 회귀선(추세선)
- 공분산 / 상관계수
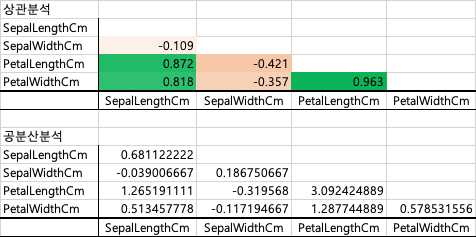
✤4 회귀 분석
- 단순 선형 회귀
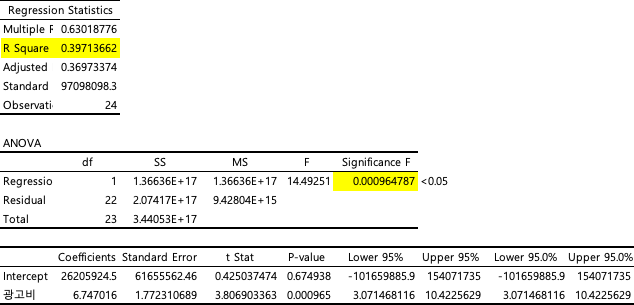
-
- 결정 계수 R : 이 모형은 전체 데이터의 약 40%를 설명한다
- 분산분석
- 귀무가설(H₀): 모든 독립변수들의 회귀계수가 0이다. 즉, 독립변수들이 종속변수에 영향을 미치지 않는다.
- 대립가설(H₁): 적어도 하나의 독립변수의 회귀계수가 0이 아니다. 즉, 독립변수들 중 적어도 하나가 종속변수에 영향을 미친다.
- 유의한 F 값이 0.05 보다 작으므로 귀무가설을 기각 - 독립변수가 종속변수에 영향을 미친다고 할 수 있다.
- 회귀식 : y = 6.747x + 26205924.531
- 다중 선형 회귀
- 조정된 결정 계수 사용 : 변수가 추가될 때마다 R²가 증가하는 문제를 보완하기 위해
- 회귀식을 만들 때 p-value가 낮은 변수를 유지하고, 높은 변수를 제거할 수 있음
- 주의사항 : 다중공선성, p-value의 한계 (p-value는 통계적 유의성만을 나타내고 실제 효과의 크기를 반영하지 않음 = p-value가 낮다고 해서 그 변수가 실질적으로 매우 중요한 변수는 아닐 수 있음)
✤5 시계열 분석
- 시간의 흐름에 따라 수집된 데이터를 분석
- FORECAST.ETS : 지수 평활법을 기반으로 시계열 데이터를 예측, 주로 데이터에 계절성이 존재하는 경우에 사용
- FORECAST.ETS(target_date, values, timeline, [seasonality], [data_completion], [aggregation])
#데이터분석 #데이터분석부트캠프 #패스트캠퍼스 #패스트캠퍼스부트캠프 #패스트캠퍼스데이터분석부트캠프
반응형
'[패스트 캠퍼스] 데이터 분석 부트캠프 16기 > 학습일지' 카테고리의 다른 글
| [패스트캠퍼스] 데이터분석 부트캠프 (8주 차) - MySQL (1) | 2024.10.11 |
|---|---|
| [패스트캠퍼스] 데이터분석 부트캠프 (4주 차) (2) | 2024.10.07 |
| [패스트캠퍼스] 데이터분석 부트캠프 (3주 차) (0) | 2024.10.07 |
| [패스트캠퍼스] 데이터분석 부트캠프 (1주 차) (0) | 2024.08.23 |
| [패스트캠퍼스] 데이터분석 부트캠프 16기 OT 후기 (0) | 2024.08.20 |